Lecture 5

Ordered Pairs and Cartesian Products

An ordered pair is best thought of as a tuple $(a,b)$ where the order matters as opposed to sets which are unordered $\{a,b\}$ (where $\{b,a\}$ is identical). The cartesian product $A\times B$ of sets $A$ and $B$ is defined as $\{(a,b):a\in A,b\in B\}$. is the set of all ordered pairs of all elements in $A$ and $B$.

For example, for the sets of vehicles $V=\{\text{car},\text{van}\}$ and colours $C=\{\text{red},\text{white},\text{black}\}$, the cartesian product is:

\begin{eqnarray} C\times V =&& \{(\text{red},\text{car}),(\text{white},\text{car}),(\text{black},\text{car}), \\ && (\text{red},\text{van}),(\text{white},\text{van}),(\text{black},\text{van})\} \end{eqnarray}

Relations

We call the subset $\Re \subseteq (A\times B)$ a relation from $A$ to $B$.

For example, consider $A=\{1,2,3,4,5,6,7,8,9,10\}$ and $B=\{1,2,3,4\}$ with relation $\Re =\{(1,4),(1,3),(1,2),(1,1),(2,4),(2,2),(3,3),(4,4)\}$. In this case, the relation $\Re$ can be written as $\Re =\{(a,b):(a\in A)\wedge (b\in B)\wedge (a\mid b)\}$ (all of $a$‘s elements are in set $A$, all of $b$‘s elements are in set $B$, and all of the elements in $a$ divides $b$). We can write $a\Re b$, or ”$a$ is related to $b$” if $(a,b)\in \Re$, for example $1\Re 4$, $1\Re 3$,…,$4\Re 4$.

Some properties of relations include: let $A$ be a set

• $\Re \subseteq A\times A$ is reflexive if for all $a\in A,a\Re a$
• $\Re \subseteq A\times A$ is symmetric if for all $a,b\in A,a\Re b\to b\Re a$
• $\Re \subseteq A\times A$ is antisymmetric if for all $a,b\in A,(a\Re b)\wedge (b\Re a)\to (a=b)$
• $\Re \subseteq A\times A$ is transitive if for all $a,b,c\in A,(a\Re b)\wedge (b\Re c)\to (a\Re c)$

Example A

Let $A=\{x,y,z\}$ and $\Re =\{(x,x),(x,y),(x,z),(y,y),(y,x),(z,x)\}$.

• $\Re \subseteq A\times A$ is not reflexive ($(z,z)$ is missing)
• $\Re \subseteq A\times A$ is symmetric (every pair also appears with the order reversed)
• $\Re \subseteq A\times A$ is not antisymmetric ($(x,y)$ and $(y,x)$ exist in the set but $x\ne y$)
• $\Re \subseteq A\times A$ is not transitive ($(y,x)$ and $(x,z)$ exist in the set but $(y,z)$ is missing)

Example B

Let $A={\mathbb{Z}}^{+}$ and $\Re =\{(x,y):(x\in {\mathbb{Z}}^{+})\wedge (y\in {\mathbb{Z}}^{+})\wedge (x\mid y)\}$.

• $\Re \subseteq A\times A$ is reflexive (every positive integer is divisible by itself)
• $\Re \subseteq A\times A$ is not symmetric ($5\mid 10$ but $10\nmid 5$)
• $\Re \subseteq A\times A$ is antisymmetric (the only integer where a divisor and a multiple of a given integer is itself)
• $\Re \subseteq A\times A$ is transitive ($a\mid b,b\mid c⟹a\mid c$)

Equivalence Relations and Partial Orders

Properties	Equivalence Relation	Partial Order
Reflexive	✅	✅
Symmetric	✅	❌
Antisymmetric	❌	✅
Transitive	✅	✅

Equivalence Relation Example

A relation that is reflexive, symmetric, and transitive is an equivalence relation. For example, we can show that $\equiv \text{mod }d$ is an equivalence relation from any non-zero integer $d$.

Recall that for integers $x$ and $y$, $x\equiv y\text{ mod }d\leftrightarrow d\mid (y-x)$.

• For any integer $x$, $d$ divides $x-x$ since zero is divisible by all non-zero integers. This implies that the relation is reflexive.
• If $x\equiv y\text{ mod }d$, then $\exists k\in \mathbb{Z}$ such that $y=kd+x$. Rearranging gives us $x=(-k)d+y$, hence $\exists k^{\prime }\in \mathbb{Z}$ such that $x=k^{\prime }d+y$ (where $k^{\prime }=-k$). This implies the relation is symmetric.
• If $x\equiv y\text{ mod }d$ and $y\equiv z\text{ mod }d$, $\exists k_1,k_2\in \mathbb{Z}$ such that $x=k_{1}d+y$ and $y=k_{2}d+z$. This gives $z-x=y-k_{2}d-x=x-k_{1}d-k_{2}d-x=(-k_1-k_2)d$, implying the relation is transitive. These three confirm that the relation is an equivalence relation.

Partial Orders

A relation that is reflexive, antisymmetric, and transitive is a partial order. For example, we can show that $\le$ is a partial order on the set of integers.

• For any integer $x$, $x\le x$. This implies that the relation is reflexive.
• Similarly, for any integers $x$ and $y$, $x\le y$ and $y\le x$ if and only if $x=y$. This implies the relation is antisymmetric.
• For any integers $x$, $y$, and $z$, if $x\le y$ and $y\le z$, then $x\le z$. This implies the relation is transitive. These three confirm that the relation is a partial order.

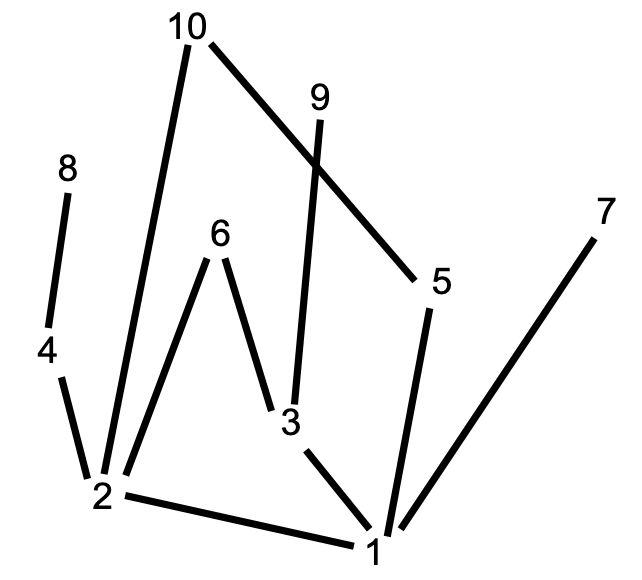
Hasse Diagrams

One way to visualise a partial ordering is a Hasse diagram. It is effectively a directed graph with the elements as nodes and directed edges denoting the relation. The graph is simplified by:

• Not including edges from an element to itself (does not show reflexivity)
• Not including transitive edges. These can be inferred
• Not explicitly including directions on the edges, rather placing that all arrows are directed upwards.

Consider the set $A=\{1,2,3,4,5,6,7,8,9,10\}$ and the relationship $a\Re b=a\mid b$. We want to visualise $5\mid 10,3\mid 9,4\mid 8,3\mid 6,2\mid 6,2\mid 4$, as well as $1$ dividing into every prime number (since every other number can be inferred transitively).

Functions

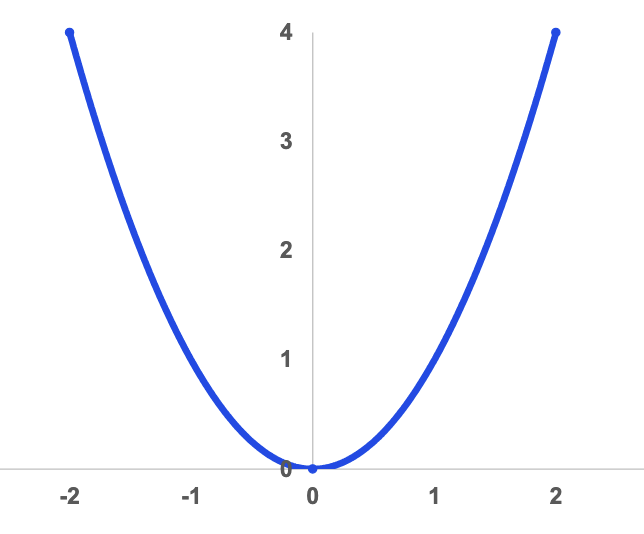
A function is a relation $f\subseteq A\times B$ where every element of $A$ appears exactly once as the first component of the ordered pair. For each $a\in A$, we have exactly one $(a,b)\in f$. We often use the notation $f(a)=b$ and can write $f:A\to B$. Consider the sets $A=\mathbb{R}$ and $B={\mathbb{R}}^{+}\cup \{0\}$ with the relation $f=\{(x,x^2):x\in A\}$. In other words, for every element $a$ in $A$, the corresponding element $b$ in $B$ in the ordered pair $(a,b)$ is the square of the value of $a$. Points in this relation include $(0,0),(0,1),(-2,4),(-0.5,0.25)$ etc.

One-to-One Functions

For sets $A$ and $B$, a function $f:A\to B$ is one-to-one if $\forall x\in A,\forall y\in A,(f(x)=f(y)\to x=y)$. Informally, this means that if the second component of two ordered pairs are the same (the outputs), the corresponding first components must be the same (the inputs). Graphically, this is obvious when it fails the horizontal line test, like the previous example. This is also verified algebraically, since $f(1)=f(-1)$ but $1\ne -1$.

Consider the linear function, for $A=\mathbb{R},B=\mathbb{R},f=\{(x,x+3):x\in A\}$. Graphically, this can be easily seen, however it can be also be proven algebraically:

\begin{eqnarray} f(x)=f(y) \implies x+3 &=& y+3 \\ x &=& y \end{eqnarray}

Onto Functions and Bijections

For sets $A$ and $B$, a function $f:A\to B$ is “onto” if $\forall b\in B,\exists a\in A$ such that $f(a)=b$.

It is easy to show that for any linear function $f:\mathbb{R}\to \mathbb{R},f(x)=ax+b$ is onto, provided $a$ is non-zero. We simply need to show that, for any $y\in \mathbb{R},\exists x$ such that $f(x)=y$. We can prove this directly by setting $x=\frac{y-b}{a}$ so that $f(x)=a(\frac{y-b}{a})+b=y$.

A function which is both one-to-one and onto is a bijection.