Lecture 1

Truth Tables

Each individual statement can be assessed to be True (1/T) or False (0/F)

• Connective and: $\wedge$
• Connective or: $\vee$
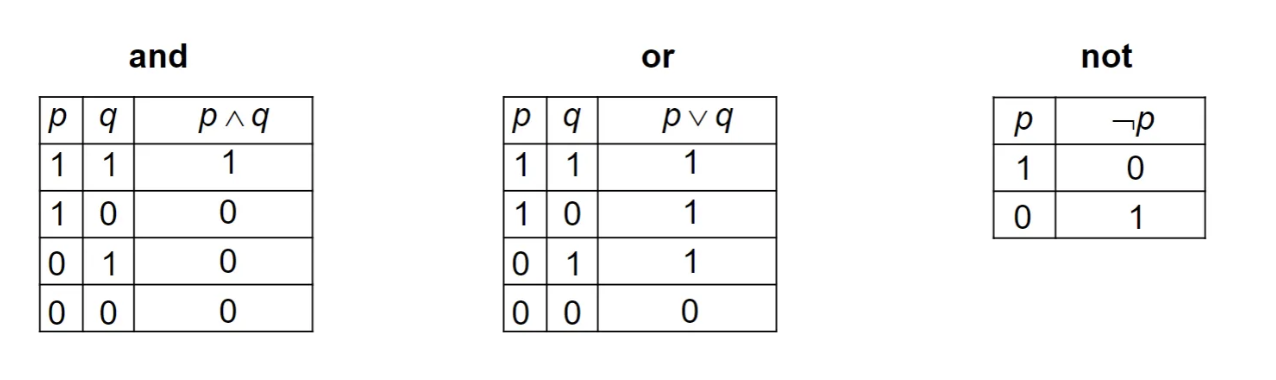
• Negation not: 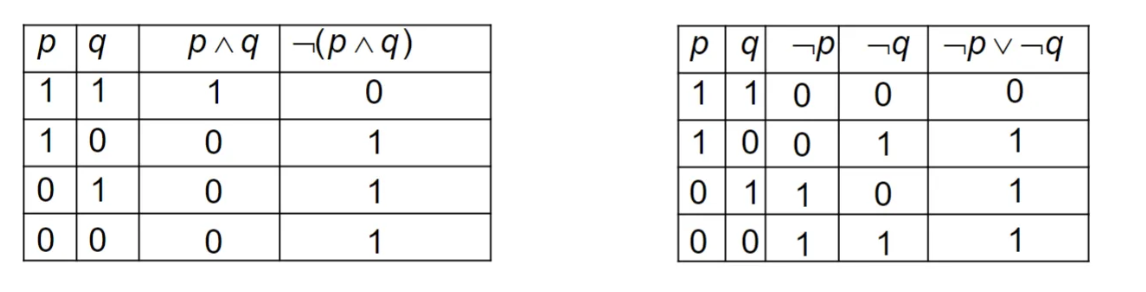$\neg$ Two statements can be logically equivalent if their truth tables have identical values. For example, $\neg (p\wedge q)$ and $\neg p\vee \neg q$ are logically equivalent above.

Implies

“p implies q”, written as $p\to q$ says “if $p$ is true, $q$ is also true”

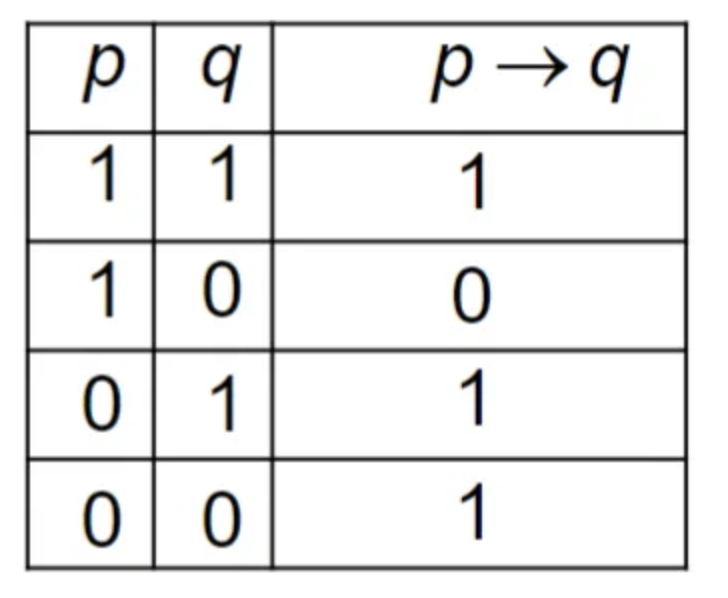
The top two rows are trivial. For the bottom rows, we have no information on $q$. By convention, since we cannot disprove the implication (if $p$ is not true), we accept that the implication (the result of $q$) is true.

Loosely translated to: if the first one is true, only if the second is also, plus all the times it’s not the first one 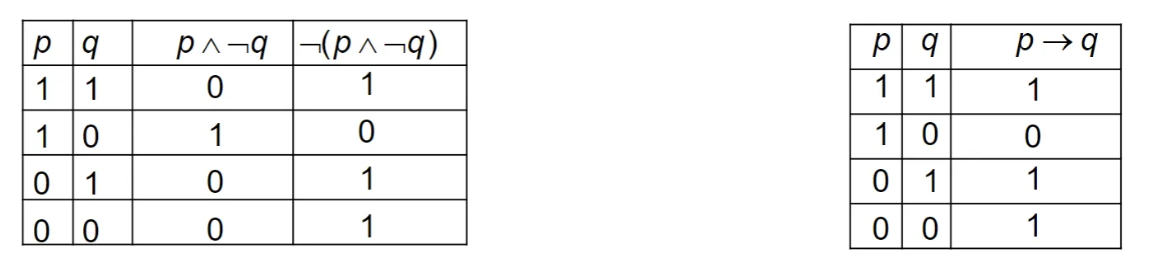Note that $p\to q$ is logically equivalent to $\neg (p\wedge \neg q)$, and similarly is logically equivalent with $\neg p\vee q$.

Tautology / Contradictions

A tautology is a statement which is always true, regardless of truth assignments. $p\vee \neg p$ is always true (I own a pet dog or I do not own a pet dog).

A contradiction is always false, regardless of its truth assignments. $p\wedge \neg p$ is always false (I own a pet dog and I do not own a pet dog).

Variables

$P(x)$: where “x is an even integer” $Q(x)$: where “x skipped breakfast this morning” (does not need to be quantitative)

Quantifiers

“For all” $\forall$ and “there exists” $\exists$

For all

Need to define the “universe of discourse” (the set of objects which the statement is defined for).

Typically can be all real numbers ($\mathbb{R}$), all positive real numbers (${\mathbb{R}}^{+}$), all integers ($\mathbb{Z}$), etc.

For example, $\forall x\in \mathbb{Z},\exists x^2\in \mathbb{Z}$ translates to “for every integer $x$, there exists a value $x^2$ which is an integer”, which is true. $\forall x^2\in \mathbb{Z},\exists x\in \mathbb{Z}$ is not true however, for example the case of $x^2=3$. If we changed the universe of discourse to be ${\mathbb{R}}^{+}$ (all positive real numbers), both statements would be true.

Negation of Quantified Statements

We need to find one counterexample.

Let $x$ be defined on the set of all dogs, and let $P(x)$ be the statement “this dog has four legs”.

The statement “Every dog has four legs” would be written as $\forall x,P(x)$.

Its negation is written as “there exists a dog which does not have four legs”, ie. $\exists x,\neg P(x)$. Therefore, the negation of $\forall x,P(x)$ is $\exists x,\neg P(x)$.

Similarly, to negate $\exists x,P(x)$, we would have to show that for all $x$, $P(x)$ is not true (ie. the negation is $\forall x,\neg P(x)$).